I had already finished the MERCIA ALU design, when Roelof Horst attended me on the pages of Dieter Mueller (http://www.6502.org/users/dieter/a3/a3_0.htm). On those pages, Dieter describes a multiplexer based ALU that is exceptional powerful and uses a very limited number of relays. Although the pages contain some errors and the sketched ALU would not work properly, the approach was sound. His ALU provides 12 useful functions using 9 SPDT relays per bit. Based on this work I was able to design an ALU with 29 useful functions, using only 8 SPDT relays per bit. Roelof Horst then suggested an improvement that reduces the ALU to 7 relays per bit (and 26 functions). When DPDT relays are used, this can be reduced to 5 relays per bit. This is the ALU that will be presented here.
An arithmetic logic unit (ALU) performs integer arithmetic and logical operations. It is common practice to design the ALU one bit at the time (bit sliced ALU). When that is done, the complete ALU is easily obtained, by putting a number of 1-bit ALU’s together and add steering logic.
The logic part
Every ALU has a logic part. For a two bit input, there are three binary functions to combine both inputs (a and b) to one output (c). These are AND, OR en XOR. When the result is inverted (0 becomes 1 and 1 becomes 0) this is notated as: NOT c or ¬c. The NOT combined with AND, OR and XOR gives NAND, NOR and XNOR. The truth tables of these functions are given below.
|
NOT a |
NOT b |
a AND b |
a OR b |
|||||||||||
|
In |
Out |
In |
Out |
In |
Out |
In |
Out |
|||||||
|
a |
b |
c |
a |
b |
c |
a |
b |
c |
a |
b |
c |
|||
|
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|||
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
|||
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
|||
|
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|||
|
a XOR b |
a NAND b |
a NOR b |
a XNOR b |
|||||||||||
|
In |
Out |
In |
Out |
In |
Out |
In |
Out |
|||||||
|
a |
b |
c |
a |
b |
c |
a |
b |
c |
a |
b |
c |
|||
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
|||
|
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|||
|
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
|||
|
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
|||
The adder (arithmetic part)
The arithmetic part of the ALU primary contains an adder. The addition of two binary values is defined by the following truth table.
|
Full adder |
||||
|
In |
Out |
|||
|
Carry |
a |
b |
c |
Carry |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
The term ripple carry is used when the value of the carry out is calculated by use of a relay that is switched on by the carry in. In that case the carry ripples through the entire word and causes a significant delay. With Mercia’s ten bit word, this means that in a worst case 10 relays must be consecutive switched on, before the carry of the most significant bit (MSB or bit 9) is calculated correctly.
It is evident that a ripple free adder is needed in order to eliminate the carry delay.
The subtractor (arithmetic part)
There are various reasons why the addition of a subtractor to an ALU is very useful. And, as will be shown, implementation can be done without using extra relays. That alone is reason enough to implement substraction in the ALU.
Subtraction in an ALU is realized by adding a negative number. So b – a is implemented as b + (– a). For negative numbers the 2-complement encoding is used. Al large advantage of 2-complement coding, is that there is only one zero and all binary functions can be used unchanged and without compromising the value. A number can be made negative by inverting the number and add one.
So: – a = ¬a + 1. The same formula applies to making a negative number positive. So the subtraction is realized by calculating: c := b – a or c := b + ¬a + 1.
|
Dec |
2com |
Hex |
Bin |
|
2com |
Dec |
Hex |
Bin |
|
0 |
0 |
0000 |
|
7 |
7 |
7 |
0111 |
|
|
1 |
1 |
1 |
0001 |
|
6 |
6 |
6 |
0110 |
|
2 |
2 |
2 |
0010 |
|
5 |
5 |
5 |
0101 |
|
3 |
3 |
3 |
0011 |
|
4 |
4 |
4 |
0100 |
|
4 |
4 |
4 |
0100 |
|
3 |
3 |
3 |
0011 |
|
5 |
5 |
5 |
0101 |
|
2 |
2 |
2 |
0010 |
|
6 |
6 |
6 |
0110 |
|
1 |
1 |
1 |
0001 |
|
7 |
7 |
7 |
0111 |
|
0 |
0 |
0 |
0000 |
|
8 |
-8 |
8 |
1000 |
|
-1 |
15 |
F |
1111 |
|
9 |
-7 |
9 |
1001 |
|
-2 |
14 |
E |
1110 |
|
10 |
-6 |
A |
1010 |
|
-3 |
13 |
D |
1101 |
|
11 |
-5 |
b |
1011 |
|
-4 |
12 |
C |
1100 |
|
12 |
-4 |
C |
1100 |
|
-5 |
11 |
b |
1011 |
|
13 |
-3 |
D |
1101 |
|
-6 |
10 |
A |
1010 |
|
14 |
-2 |
E |
1110 |
|
-7 |
9 |
9 |
1001 |
|
15 |
-1 |
F |
1111 |
|
-8 |
8 |
8 |
1000 |
Other functions (arithmetic part)
There are some other functions that are very useful to have available in the ALU.
Incrementing can be realized by adding one to a or c := a + 1. Therefore the carry input of the least significant bit can be used. This input carry is normally not used. But since is there, it can be made useful. Since the adder normally adds both inputs (c := a + b + 1), b must be removed from the addition.
Negation (c := – a ) can be realized in the same way as incrementing, only the value of a has to be inverted first (c := ¬a + 1).
Decrementing is very useful for loop control. Looping x times, is best done by starting with x and decrement by 1 until zero is reached. Checking for a zero is default ALU functionality. For the alternative, starting by 1 and adding 1 until x is reached, far more instructions are needed. Decrementing must be done by adding -1 to a. In 2-complement encoding, -1 is represented by a value with only ones. This can be accomplished by setting all the bits in the word to 1. So c := a – 1 is implemented by c := a + 1111111111. For decrementing, b must be removed from the addition and each and every bit a 1 has to be added.
Shift left and shift right are essential functions for multiplication. Multiplication of binary numbers is done exactly the same way as decimal numbers, as shown in the following example (11 * 5 = 55):
|
1 |
0 |
1 |
1 |
|||
|
|
|
|
1 |
0 |
1 |
* |
|
1 |
0 |
1 |
1 |
|||
|
0 |
||||||
|
1 |
0 |
1 |
1 |
|
|
+ |
|
1 |
1 |
0 |
1 |
1 |
1 |
For every step of this multiplication, the:
- multiplicand is shifted left;
- next bit of multiplier is examined (also a shifting step, namely shift right);
- if this next bit is 1, the shifted multiplicand is added to the product.
MERCIA’s ALU is able to perform the following functions.
|
|
a + 1* |
|
|
b + 1* |
|
|
a + b |
|
|
a + b + 1* |
|
|||||||||||
|
|
In |
|
Out |
|
In |
|
Out |
|
In |
|
Out |
|
In |
|
Out |
|||||||
|
Car |
a |
b |
c |
Car |
Car |
a |
b |
c |
Car |
Car |
a |
b |
c |
Car |
Car |
a |
b |
c |
Car |
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|||
|
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
|||
|
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
|||
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|||
|
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
|||
|
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
|||
|
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||
|
|
-a* |
|
|
-b* |
|
|
a - 1 |
|
|
b - 1 |
|
|||||||||||
|
|
In |
|
Out |
|
In |
|
Out |
|
In |
|
Out |
|
In |
|
Out |
|||||||
|
Car |
a |
b |
c |
Car |
Car |
a |
b |
c |
Car |
Car |
a |
b |
c |
Car |
Car |
a |
b |
c |
Car |
|||
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|||
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|||
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|||
|
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
|||
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|||
|
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
|||
|
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
|||
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||
|
|
a - b |
|
|
b - a |
|
|
Shift left a |
|
|
Shift left b |
|
|||||||||||
|
|
In |
|
Out |
|
In |
|
Out |
|
In |
|
Out |
|
In |
|
Out |
|||||||
|
Car |
a |
b |
c |
Car |
Car |
a |
b |
c |
Car |
Car |
a |
b |
c |
Car |
Car |
a |
b |
c |
Car |
|||
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
|||
|
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
|||
|
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
|||
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|||
|
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
|||
|
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
|||
|
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||
*Carry in bit 0 must be set to 1
|
|
-1 |
|
|
0 |
|
|
a |
|
|
b |
|
|||
|
In |
Out |
In |
Out |
In |
Out |
In |
Out |
|||||||
|
a |
b |
c |
a |
b |
c |
a |
b |
c |
a |
b |
c |
|||
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
|||
|
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
|||
|
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|||
The MERCIA ALU
The relay ALU that I designed for MERCIA, is shown below. It has 26 functions and (only) 7 relays per bit.
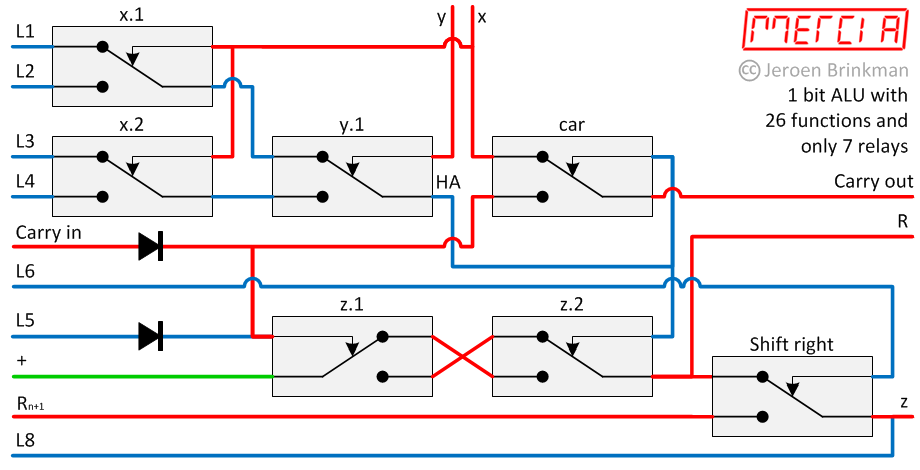
The working of this carry free ALU is simple but ingenious. HA resembles the result of the multiplexer based logic unit with condition lines L1 to L4. In order to eliminate the influence of the carry during logic instructions, L5 is used to set all the carry bits to 1. If L5 is 1, then R=HA.
To understand the construction of this ALU, it helps to keep this logic table of an adder in mind.
|
In |
Out |
||||
|
Carin |
x |
y |
HA |
z |
Carout |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
0 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
0 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
1 |
1 |
HA resembles the result of a half adder or XOR logic function. The full adder (R) can be obtained by HA XOR Carin. This is done by the relays z.1 and z.2.
When HA is 0, Carout equals either x or y. therefore relay car is connected to y. When HA is 1, the Carout equals Carin.
When all inputs are set to 0, all the outputs (carry, R and z) will also be 0. Unfortunately the ALU can produce spikes on the z output, because z.1 and z.2 are not switched at the same moment. This can be solved by making the ALU latching. Since shift right could not be realized with the available logic, a separate relay has been added to make this available.
This ALU is controlled by 9 control signals as specified below.
|
Control |
Meaning |
|
L0 |
Add 1 by set carry in LSB to 1 |
|
L1 |
Logic feed LSB |
|
L2 |
∙ |
|
L3 |
∙ |
|
L4 |
Logic feed MSB |
|
L5 |
Set all carry in to 1 |
|
L6 |
Enable shift right |
|
L7 |
Enable circular shift |
|
L8 |
Set output LSB to 1 |
The following functions can be realized by setting the corresponding control signals.
|
|
ALU Control signals |
||||||||||||
|
Nº |
Used |
Func |
Oper |
Operation |
L0 |
L1 |
L2 |
L3 |
L4 |
L5 |
L6 |
L7 |
L8 |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
9 |
10 |
11 |
12 |
|
1 |
|
-1 |
0 |
z := -1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
2 |
0 |
0 |
z := 0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
|
|
3 |
1 |
0 |
z := 1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
|
|
4 |
x |
1 |
z := x |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
|
|
5 |
y |
1 |
z := y |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
|
|
6 |
0000 |
¬x |
1 |
z := NOT x |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
|
7 |
¬y |
1 |
z := NOT y |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
|
|
8 |
0001 |
AND |
2 |
z := x AND y |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
|
9 |
0011 |
OR |
2 |
z := x OR y |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
10 |
0101 |
XOR |
2 |
z := x XOR y |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
11 |
0010 |
NAND |
2 |
z := x NAND y |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
12 |
0100 |
NOR |
2 |
z := x NOR y |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
|
13 |
0110 |
XNOR |
2 |
z := x XNOR y |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
|
14 |
0111 |
INCx |
1 |
z := x + 1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
15 |
INCy |
1 |
z := y + 1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
|
16 |
1010 |
Add |
2 |
z := x + y |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
17 |
Addl |
2 |
z := x + + 1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
|
- |
-x |
1 |
z := -x (¬x+ 1) |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
18 |
1001 |
-y* |
1 |
z := -y (¬y + 1) |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
19 |
1000 |
x-1 |
1 |
z := x - 1 (x + 1111111111) |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
- |
y-1 |
1 |
z := y - 1 (y + 1111111111) |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
20 |
1011 |
x-y |
2 |
z := x - y (x + ¬y + 1) |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
- |
y-x |
2 |
z := y - x (y + ¬x + 1) |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
21 |
1100 |
SLx |
1 |
z := Shift left x |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
- |
|
SLy |
1 |
z := Shift left y |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
22 |
1101 |
SRx |
1 |
z := Shift right x |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
|
23 |
SRy |
1 |
z := Shift right y |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
|
24 |
1110 |
SCLx |
1 |
z := Shift circular left x |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
- |
|
SCLy |
1 |
z := Shift circular left y |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
25 |
1111 |
SCRx |
1 |
z := Shift circular right x |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
|
26 |
|
SCRy |
1 |
z := Shift circular right y |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
* only if x=0
Since the register select (described in the following paragraph) is able to connect every register with the inputs a as well b, only the functions are used which use a as an operand. Those functions are marked in the column ‘used’.
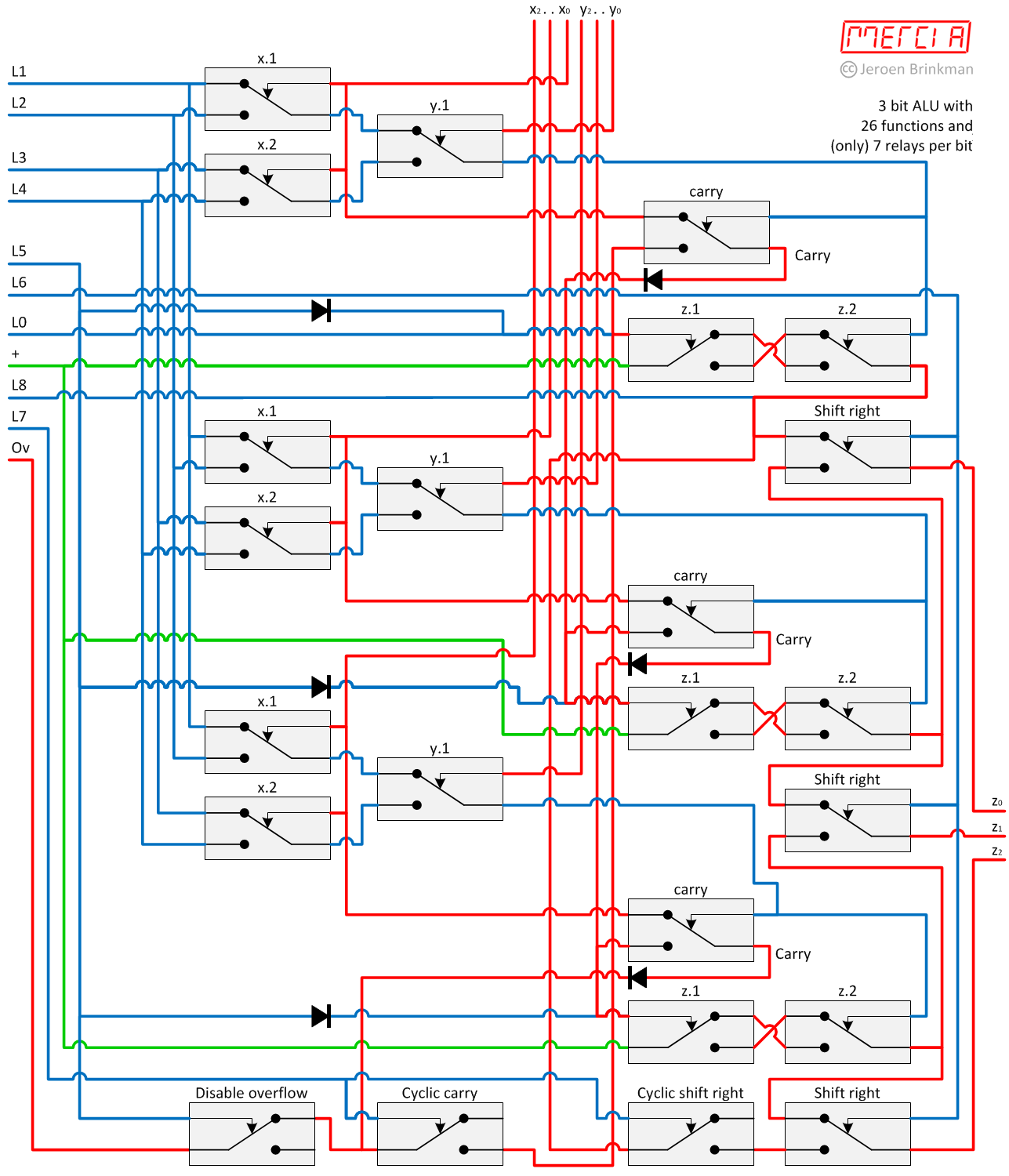
An example of a three bit ALU is drawn in the following circuit diagram. On top of the diagram the LSB (bit 0) and on the bottom the MSB (bit 2). To scale up this ALU to the full 10 bits, bit 1 is repeated eight times.
The ALU register controller
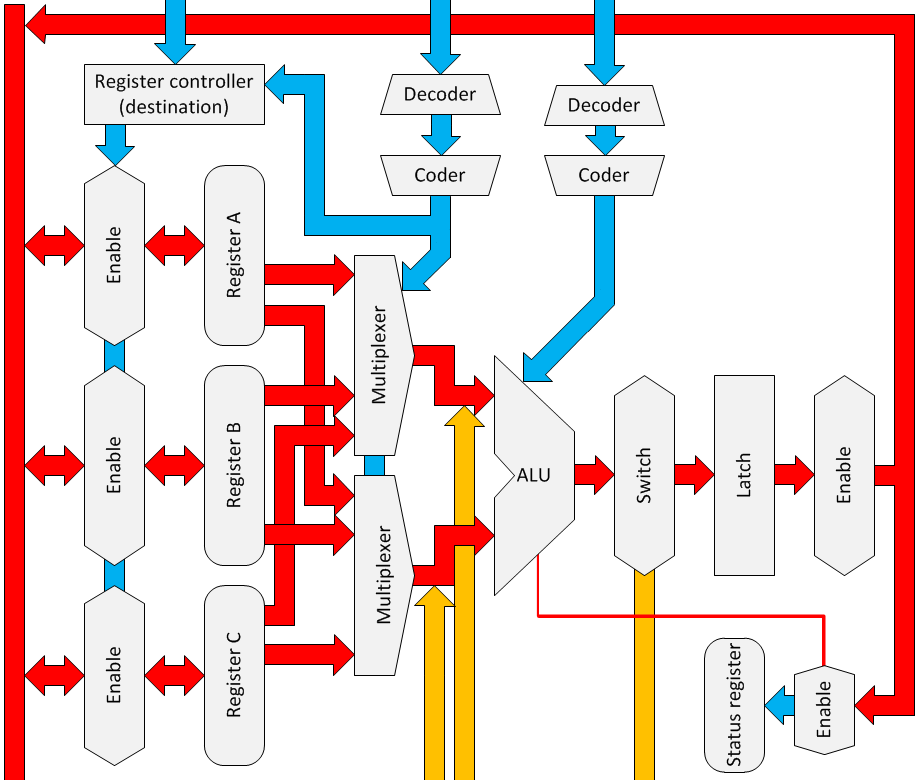
The register controller controls the in- and output of data to the ALU.
It is very common to perform several ALU operations after each other. Think of shift functions or logical operations. Not all the ALU operations are symmetrical. Symmetrical means the input operands a and b may be switched. For instance a + b is symmetrical, because it is equal to b + a. Subtraction, a – b is not and all the unary operations (operations only on a) are also not symmetrical. Therefore it is very handy to use the output of the first ALU operation as input for the second operation. This can be done by selecting which register should be mapped on x and which on y.
There are six possibilities to map three registers (A, B and C) on two inputs (x and y) and one output (z):
xy z
abÒc
acÒb
baÒc
bcÒa
caÒb
cbÒa
Since the command and ALU-operation coding both takes four bits, there are only two bits available for the register usage coding. That means that only four of these possibilities can be implemented. When multiplications must be done, this will slow down the execution speed because values of registers need to be swapped and swapping takes 6 microcode steps.
In order to avoid this and improve speed, three improvements are made:
1. Two ALU commands are used. Then there are 3 bits available for register usage coding or eight register usage coding possibilities.
2. The ALU is made latching. That means it can hold its output result for a while, and therewith makes it possible to write to one of the input registers. In other words, operations with one operand (shifting, incrementing) do not need a second register. The multiplication shift operation on both operands will benefit from this, because register swapping is not needed.
3. caÒb is replaced by caÒc, in order to make repeated addition and subtraction possible.
This results in the following table.
|
Opcode |
Input x |
Input y |
Output z |
||||||||||
|
Nº |
Operation |
Bit6 |
Bit5 |
Bit4 |
a→x |
b→x |
c→x |
a→y |
b→y |
c→y |
z→a |
z→b |
z→c |
|
1 |
aÒa |
0 |
0 |
0 |
1 |
0 |
0 |
- |
- |
- |
1 |
0 |
0 |
|
2 |
abÒc |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
3 |
acÒb |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
4 |
bÒb |
0 |
1 |
1 |
- |
- |
- |
0 |
1 |
0 |
0 |
1 |
0 |
|
5 |
baÒc |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
6 |
bcÒa |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
7 |
caÒc |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
|
8 |
cbÒa |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
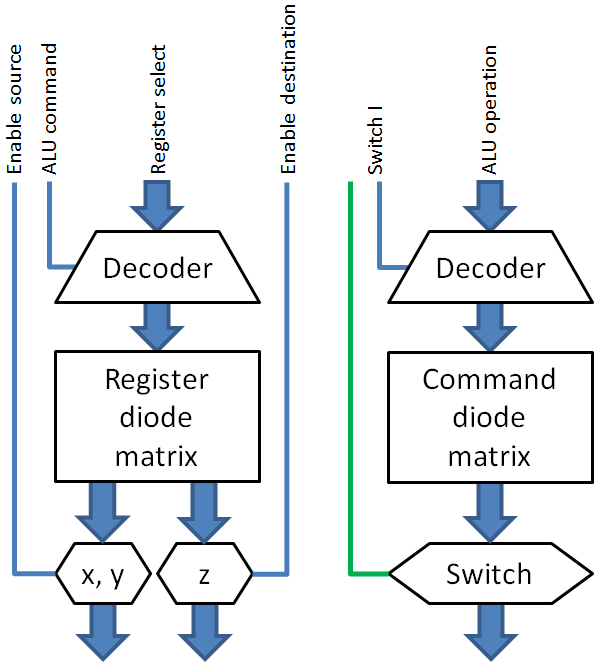
The different signals can be generated by a 3-bit coder and diode matrix decoder.
For the input, the register control activates the registers as shown below (one bit only).
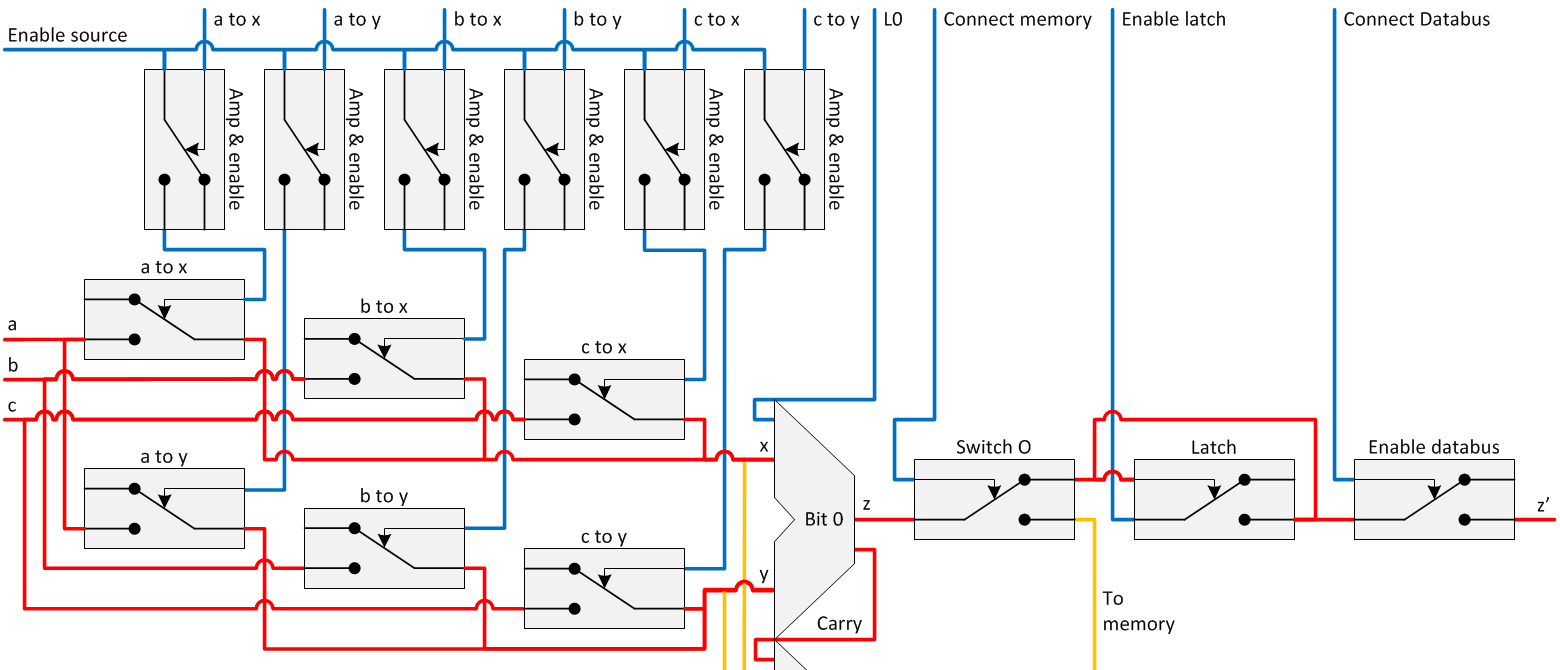
The diode matrix can handle a limited amount of current. Therefore amplifiers are needed. These amplifiers are combined with a switch and controlled by the:
- enable source signal that activates the source registers;
- enable destination signal that activates the destination register;
- switch I signal that also activates the ALU;
- ALU command signal that routes the ALU operation in the instruction to the ALU
all originating in the instruction decoder.
MERCIA uses relative addressing. This enables the possibility to place a program on any position in the memory, without changing it. The first byte of a program is set as memory position 0. All addressing then can be done relative to this first byte. In order to effectuate that, the position of the first byte must be added to referred address. The yellow lines and output switch facilitate this function.
The latch makes it possible to store the output function of the ALU in one of the input registers. This function speeds up multiplications en increases the efficiency of the input registers because they can hold three values instead of two.
The ALU switch increases the speed of the computer’s microcode, because the databus is free for other data traffic, while the result is stored in the latch.
The ALU command controller
Finally the ALU has to be controlled by the Computer’s control logic. The 16 ALU commands takes 4 bits of the instruction word. A 4 bit to 16 lines decoder in combination with a 16 lines to 9 lines encoder are used to generate the 9 control signals the ALU uses. For this encoder a standard 16*40 bit DIP-switch ROM card is used. The last 28 bits are used to encode a four digit 7-segment display that shows the ALU function that is active.
The use of a DIP-switch ROM card for the command decoding, makes the decoding very flexible. As a matter of fact, one of the 16 commands could be replaced by another command, just by changing the DIP-switch settings. This makes it possible to adjust the ALU, so that the most used and therewith most effective functions can be selected. Because the current that may run through the dipswitches and diodes is limited, amplifiers are placed when more than one relay needs to be switched.
The complete ALU is sketched in the block-diagram below.
Relay count
A total of 16 relays/poles per bit are needed for the complete ALU. An additional 45 relays are needed to control the ALU and implement the status register.
|
Bit related |
Relays |
|
General |
Relays |
|
Input select |
6 |
|
Command decoder |
15 |
|
ALU |
7 |
|
Register decoder |
7 |
|
Switch o |
1 |
|
Amplifiers |
18 |
|
Latch |
2 |
|
Status register |
10 |
|
Switch i |
1 |
|
Generic logic |
4 |
|
Total |
17 |
|
Total |
54 |
Together with the general – not bit related - control relays, the total relay count is 224 single pole double throw relays. The ALU as designed will not only perform the 16 ALU functions, it is also able to perform the incrementing of the program counter and to calculate the relative memory addresses.Therewith it is a very efficient implementation for the functions it delivers.
August 2015, Jeroen Brinkman